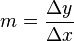Cálculo de la pendiente de una recta
Introducción
HOLA!!!!.... bienvenidos a esta página, fue creada por cuatro alumnos de 2º año medio de el Liceo Simón Bolívar con el fin de ayudarlos a aprender mas sobre matemática.... espero que esta página los ayude más en esta asignatura, gracias por visitar nuestro blog... Adiós (:
viernes, 15 de abril de 2011
Ejercicios de Plano Cartesiano
Hallar el perímetro del cuadrilátero cuyos vértices son:
A (-3,-1); B (0,3); C (3,4) y D (4,-1).
Instrucciones:
1-. Calcular las distancias de cada lado del cuadrilátero.
2-. Por ultimo, para hallar el perímetro se suman las distancias de cada lado.
P = Suma de los lados
Tipos de pendientes
| Dada una recta, gráficamente su pediente nos da su grado de inclinación. | ||
Pendiente positiva | Pendiente negativa | |
 |  | |
|
Pendiente nula | |
Cuando la recta es constante se dice que tien pendiente nula, en la expresión analítica m=0
definicion de la pendiente
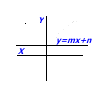
La pendiente de una recta en un sistema de representación triangular (cartesiano ), suele ser representado por la letra m, y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe:
Dados dos puntos (x1,y1) y (x2,y2), la diferencia en X es x2 − x1, mientras que el cambio en Y se calcula como y2 − y1. Sustituyendo ambas cantidades en la ecuación descrita anteriormente obtenemos:
Si la pendiente (m)es mayor que 0 se dice que la pendiente es positiva, si la pendiente es menor que 0 se dice que la pendiente es negativa, si la pendiente es igual a 0 la recta es paralela al eje (x) del plano cartesiano, y si la pendiente es indefinida la recta es paralela al eje (y) del plano cartesiano
Dados dos puntos (x1,y1) y (x2,y2), la diferencia en X es x2 − x1, mientras que el cambio en Y se calcula como y2 − y1. Sustituyendo ambas cantidades en la ecuación descrita anteriormente obtenemos:
Si la pendiente (m)es mayor que 0 se dice que la pendiente es positiva, si la pendiente es menor que 0 se dice que la pendiente es negativa, si la pendiente es igual a 0 la recta es paralela al eje (x) del plano cartesiano, y si la pendiente es indefinida la recta es paralela al eje (y) del plano cartesiano
EL PLANO CARTESIANO
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las "X" y de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se como:

Fracciones equivalentes
Dos fracciones son equivalentes cuando representan a un mismo número.
Si dos fracciones son equivalentes se verifica que el producto cruzado es igual, es decir, dadas dos fracciones son equivamentes si y sólo si
son equivamentes si y sólo si  .
.
Las siguientes fracciones son equivalentes

Determinar una fracción equivalente a una dada conocido el numerador.
Dada la fracción halla una equivalente cuyo numerador sea 12
halla una equivalente cuyo numerador sea 12

La fracción equivalente es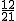
Determinar una fracción equivalente a una dada conocido el denominador.
Dada la fracción halla una equivalente cuyo denominador sea 15
halla una equivalente cuyo denominador sea 15

La fracción equivalente es
Si dos fracciones son equivalentes se verifica que el producto cruzado es igual, es decir, dadas dos fracciones
Las siguientes fracciones son equivalentes
Determinar una fracción equivalente a una dada conocido el numerador.
Dada la fracción
La fracción equivalente es
Determinar una fracción equivalente a una dada conocido el denominador.
Dada la fracción
La fracción equivalente es
Determina el valor de x para que las fracciones sean equivalentes
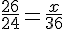
Solución x=
Suscribirse a:
Comentarios (Atom)